Hey, they did it! People have known for a long time that in 4 dimensions you can pack equal-sized balls so that each touches 24 others. In 2008 someone showed that's the best you can do. But in April this year, three mathematicians showed there's essentially just 𝑜𝑛𝑒 𝑤𝑎𝑦 you can accomplish this!
This way is easy to describe. Take the points whose coordinates are all integers, together with those whose coordinates are all integers plus 1/2. Use each of these points as the center of a ball of radius 1/2. Then each ball touches 24 others. This pattern is called the 𝗗𝟰 𝗹𝗮𝘁𝘁𝗶𝗰𝗲.
The new result shows that if you pack equal-sized balls in 4 dimensions so that each touches 24 others, you're 𝑓𝑜𝑟𝑐𝑒𝑑 to create a version of the D4 lattice - possibly rotated, translated and/or rescaled.
This sort of thing is hard to show: it took a lot of fancy math and two weeks of calculation on a standard desktop computer. I believe only other dimensions where we know a result like this are 1, 2, 8 and 24. In dimension 3 it's just false: you can pack equal-sized balls so that each touches 12 others, and this is the best you can do, but there are uncountably many different ways to do it!

Optimality and uniqueness of the $D_4$ root system
We prove that the $D_4$ root system (the set of vertices of the regular $24$-cell) is the unique optimal kissing configuration in $\mathbb R^4$, and is an optimal spherical code.arXiv.org
















mnl mnl mnl mnl mnl
in reply to modulux • • •modulux
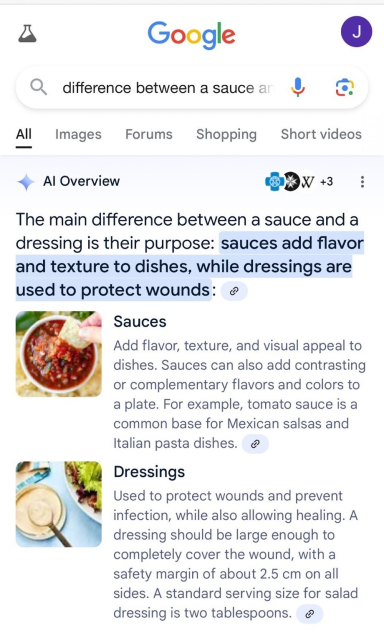
in reply to mnl mnl mnl mnl mnl • • •I tend to think so too. I suppose it shouldn't really surprise me, but I expected a bit more critical engagement.
There's lots of evidence on the limits of LLM reasoning, as well as pretty basic self-reference and so on (how many letters l does this statement include?). And yes, reasoning is being used rather technically in the sense of deductive inference.